We can define Hamiltonian Path Problem (HPP) as one graph problem, which has a computational complexity of NP-Complete. HPP consist mainly in one path in a directed or undirected graph that visits each vertex (city) exactly once. Each HPP of n vertex has (n!) different sequences of vertex might be Hamiltonian paths in an n-vertex graph (It is called graph complete). Obvious way could be use any brute force algorithms to solve any HPP, but that test all possible solutions would be a slow, for example, suggesting, we have HPP of 50 vertices, we need factorial of fifty combinations of these vertices, which are possible solutions or Hamiltonian Path, by this reason, it is necessary to check one per one all combinations to find all truth Hamiltonian path, being a hard work and sometime impossible to do with sequential computers. There are several theoretical approaches to simplify this calculation as: dividing graph edges [19], other approach is using dynamic programming (algorithm of Bellman), where this algorithm finds all shortest paths [20]. In the same way, we can find in Ford’s work [21], Moore [22] and Yen [23] other useful approach to solve graph problems.
In 1994, Professor Adleman
demonstrated a proof-of-concept, using DNA as way to compute any hard
problem, in particular the HPP of seven cities. Adleman solve a HPP,
where there is a path from city origin to city destination passing
each vertex exactly once.
This algorithm has computational complexity of O (n) bio-process and one space complexity of n! DNA strands. Also we need for 100 nodes graph almost 15 1018 millions of tonnes in organic material (DNA), in consequences impossible to manipulate and calculate any huge problem with this methodology.
On the other hand, there are parallel and distributed implementations for the solution of the HPP, using a cluster of computers, but normally, they need a huge amount of resources and communications between them, finally we can limitations to solve big problems, using these solutions. By this reason, in this article, we could show other alternative solution, using electronic components and all knowledge of DNA computing (without its chemical procedures).
This algorithm has computational complexity of O (n) bio-process and one space complexity of n! DNA strands. Also we need for 100 nodes graph almost 15 1018 millions of tonnes in organic material (DNA), in consequences impossible to manipulate and calculate any huge problem with this methodology.
On the other hand, there are parallel and distributed implementations for the solution of the HPP, using a cluster of computers, but normally, they need a huge amount of resources and communications between them, finally we can limitations to solve big problems, using these solutions. By this reason, in this article, we could show other alternative solution, using electronic components and all knowledge of DNA computing (without its chemical procedures).
The advantage that inorganic
DNA (Inchrosil [24] [25]) has compared with sequential technologies
is the great parallelism in the embodiment of the operations and it
is possible to create complex structures to solve combinatorial
problems, because Inchrosil can represent any DNA structure (simple
strand, double strands, with holes, etc). In particular at HPP, with
Inchrosil, we can create same environment of Adleman’s experiment,
by this reason and based on the aforementioned characteristics,
Inchrosil can create simple strand to codify any vertex and edge of
Hamiltonian path and can solve in parallel any problem.
As we said before, HPP is a NP
hard complete problem, being very difficult to solve with any
deterministic algorithm with polynomial order, by this reason, it is
better to use non-deterministic problem to solve any HPP, one example
of non-deterministic algorithm is presented next lines:
Where Inputs are: Graph, V in
and V out
- All paths existing in the graph are generated randomly.
- All the paths don’t contain the inputs are eliminated.
- All those paths which do not have the required vertices are also eliminated.
- For each vertex, the paths are rejected which do not include the actual vertex.
Where possible outputs are:
YES (If paths exist) NO (otherwise)
Therefore, in a conventional
computer system, normal computational time cannot be polynomial,
because it is necessary to compare all the cities one by one to find
the path from one initial city (Vin)
to one final city (Vout).
The electronic system described below was approached from the seven
(7) vertices and eleven (11) edges graph as one initial
proof-of-concept, we can see in Figure 1, seven node graphs, but it
is possible with this system a huge system with lot nodes.
Figure 1: Complete Graph OF HPP.
First step is encoding the
graph of Figure 1, using cod-Inchrosil code [24], where each city
(vertex) had number of nucleotides in its codification, i.e.
following the Adleman´s experiment, 20 nucleotides. On the other
hand, the edges are composed of the same number, 20 nucleotides,
which correspond to last nucleotides of origin city and the initial
10 nucleotides of destination city (next Figure 2 shows the
codification from City I to City J).
Figure 2: Codification Vertex I and J.
With above codification, it is
possible to create one DNA strand, which contains all vertex and
edges of graph (Figure 1). With this DNA strand would offer the
possibility, that in worst case to find a solution, it is necessary
to compare a complete graph (we can define a graph complete as one
graph, which contains all edges possible, G= (V, VxV), being before
V, the set contain all vertices of graph), and in the best case, only
graph showed in Figure 1. This possibility offers some final
programmer/user to choose one specific codification of graph (i.e.
number of edges and vertex), always inside of limits at graph. For
example, in our case, there is a DNA chain of 5040 nucleotides
(factorial of seven, because there are seven cities in our graph), by
this reason, final programmer/user could activate only complementary
part of this DNA chain in specific edges at graph to analyze. In this
case, when we are looking for Hamiltonian path, only we search a
complementary part in those specific edges.
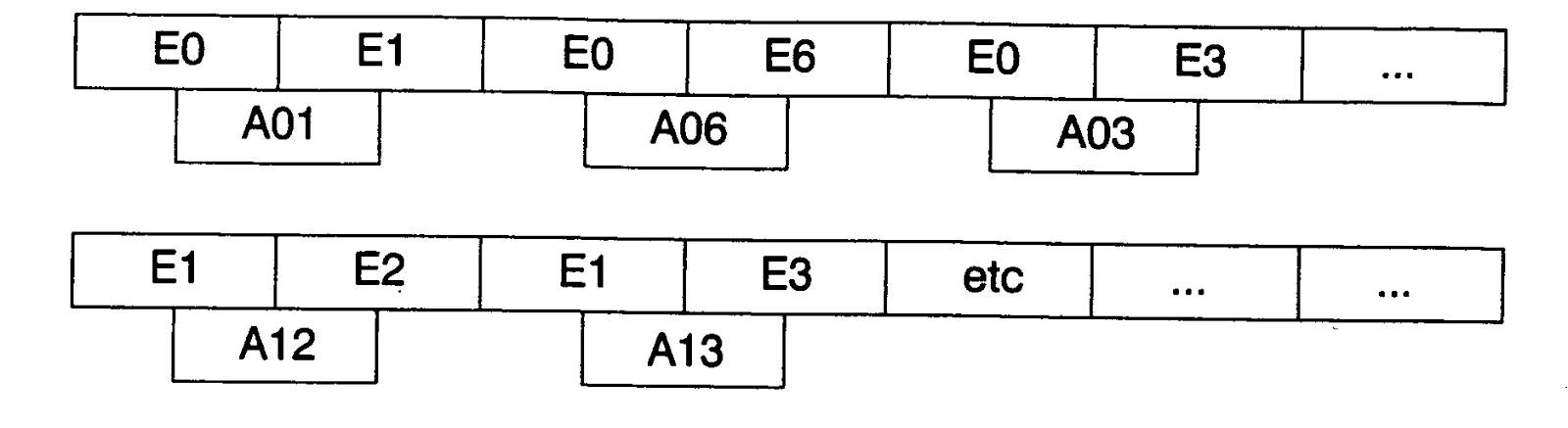
In the same way, Figure 3
shows a codification of graph, which has been codified by DNA, where
 represent vertex (in this case, cities) and
represent vertex (in this case, cities) and
 represent edges (roads between cities). On the other hand, graph of Figure 1
would be called ‘G’ and its encoding could be seen in Figure 3,
where A0…An
represents edges of graph and E0….En
represents cities or nodes of problem formulated.
represent edges (roads between cities). On the other hand, graph of Figure 1
would be called ‘G’ and its encoding could be seen in Figure 3,
where A0…An
represents edges of graph and E0….En
represents cities or nodes of problem formulated.
Figure 3: Graph Codified by DNA.
Next step consists to arrange
all the possible Hamiltonian paths inside of a seven vertices graph
complete, by this reason, using cod-Inchrosil was created a set of
5040 DNA chains (factorial of seven), with strand length of 140
nucleotides (if problem has seven cities and each city has
codification of 20 nucleotides, final strand length is 140
nucleotides). All this set of strand are organised by matrix form,
because, it was more convenient to be able to approach a final
three-dimensional chip, and in this way to emulate the nature,
finally this matrix is called ‘CG’ in our experiment.
On the other hand, in set
theory [26] is normally used to delimit the scope of a proposal, to
compare if some object is part or not of one specific set, i.e. one
set ‘S’ is defined as “YES”/ ”NO”, if and only if for
some object α in included or not in ‘S’. In our case, we can
compare each edge of ‘CG’ matrix with each specific edge in ‘G’
graph. All this operation can do in parallel way and the same time
can obtain all edges are included in ‘G’ graph. Being each edge
of ‘CG’ object need be compared with edge set proposal for
programmer to determine which of these edges are included in ‘G’,
remember, ‘CG’ is all possible solutions of the problem. As it is
described in [24], Inchrosil is an electronic circuit allows storing
all information of one pair of nucleotides by binary form, you can
see Figure 4. This minimal unit allows create complex form or set of
nucleotides (activating or not complementary chain), in our example
all chains of ‘G’ graph and ‘CG’ matrix.
Figure 4: Inchrosil Unit
Above, we have described a
parallel comparison between ‘CG’ matrix and ‘C’ graph to find
all possible edges included in ‘C’. To be able to perform these
comparisons in our experiment is necessary to use the philosophy of
logical half-adders [27], carry-save adders (CSA) and Wallace trees.
Highlight, for our experiment is removed carry option in massive
comparison, doing direct additions of two inputs. On the other hand,
following truth table of XOR gate, when two inputs are the same
result, final result is 0, by this reason, in our experiment we have
considered to invert all outputs, being 1 in all positive case and 0
in all negative case. Due to this approach, comparers were developed
with XNOR gates to resolve the problem, by this reason; in our
experiment, we have joined together 40 XNOR gates, where if each edge
has 20 nucleotides, being 40 bits per edge and 80 bits of inputs,
since it will be compared two by two. With this system, it is
possible to create CSA without carry, where joining all XNOR gates
would giving a unique result of 40 bits.
Finally, the system offered a
40 bits result, which was not optimum to specify one edge is the same
or not, because final answer should be ‘yes’ or ‘no’ (i.e. 0
or 1). In this case, we needed a system to check all input and to
generate only one output, by this reason, using only AND gates, we
were able to create a system, which has 40 inputs and only one
output, where system gives a ‘1’ as logical result, this result
would mean that both edge are the same, on the other hand, if logical
result is ‘0’, both edges are different. In case of positive
result, edge is part of ‘G’ graph (which is a possible
Hamiltonian path).
This process could be
parallel, by this reason, all comparer are distributed by one matrix
form to compare by parallel way, all edge (two to two) in twice
systems (‘G’ graph and ‘CG’ matrix). Highlight, with this
system we can obtain if one edge is contained in ‘G’ graph
solution, but with this sub-method do not indicate yet, if ‘G’
graph solution is a Hamiltonian Path, by this reason, in our
experiment, we have used sub-method of Wallace trees methodology
[28]. In general, they have same philosophy of Wallace Trees, but
some specific customizations in their structure, i.e. we have created
one for each sub-result of comparison (column of matrix). These
systems are composed by OR gates, creating with this way, several
levels as Wallace trees to find all possible coincidences between
edges and chains.
The final objective is to find
one chains where all edges have coincidences, in this case, we would
have a Hamiltonian Path. That is possible because all outputs of OR
gate system are connected with other system compose for AND gates and
only one output, which indicates ‘YES’ or ‘NO’ the possible
solution is Hamiltonian path.
Finally, we can obtain a
vector with n components (being n in our case, 5040 chains), where
one element of vector has ‘1’ logical value, this element
indicates is Hamiltonian path. In this case, we considered tp
as time to create all possible solutions, tc
as time to
compare all edges of one component, tf
as time to compare all sub-results, ta
as additional time (delays in gates, communications, check final
vector, etc.) and finally, n as number of components, we can
formulated final time is T = tp
+ n tc
+ tf
+ ta,
being this time close to polynomial order, because before times are
considered in polynomial order.
On the other hand, due
modularity of the system, it is possible to create complex structures
or system with huge number of nodes, because we can create circuit to
solve partial solutions and later to join all solution to find final
solution.
In Figure 5,
we can see all circuit to calculate any Hamiltonian path of 7 cities,
where the reference Figure 5-18 is ‘CG’ matrix with all possible
Hamiltonian paths, the reference Figure 5-12 is the module, which
compares edges between ‘CG’ and ‘C’, references Figure 5-15
and Figure 5-16 are logical gates to calculate similarity between DNA
chains and finally, the reference Figure 5-20 is a vector with all
comparison.
Figure 5: Hamiltonian Path Circuit
References
[1] Sanjeev Arora and Boaz Barak, Computational Complexity: A Modern Approach, Cambridge University Press, 2009.
[2] Hopcroft John E., Motwan Rajeev, Ullman Jeffrey D, Introduction to Automata Theory, Languages, and Computation, Prentice Hall, 2007.
[3] A. Gibbons, Algorithmic Graph Theory, Cambridge University Press, 1985.
[4] F. Harary, Graph Theory, Perseus Books, 1994.
[5] L. Euler, Solutio Problematis ad geometriam situs, 1736.
[6] E. W. Dijkstra, A note on two problems in connexion with graphs, Numerische Mathematik, p. 269–271, 1959.
[7] R. W. Floyd, Algorithm 97: Shortest Path, Communications of the ACM 5 (6), p. 345, 1962.
[8] S. Warshall, A theorem on Boolean matrices, Journal of the ACM, p. 11–12. 1962.
[9] John von Neumann, First Draft of a Report on the EDVAC, 1945.
[10] J. D. Markgraf, The Von Neumann bottleneck, 2007.
[11] Jordan Baumgardner, Karen Acker, Oyinade Adefuye and Samuel Thomas Crowley, Solving a Hamiltonian Path Problem with a bacterial computer, Journal of Biological Engineering, 2009.
[12] Leonard Max Adleman, Molecular computation of solutions to combinatorial problems, Science, p. 1021–1024, 1994.
[13] Liu W, Gao L, Liu X, Wang S and Xu J, Solving the 3-SAT problem based on DNA computing, 2003.
[14] Gheorghe P˘aun, Introduction to Membrane Computing, 2009
[15] Mihai Oltean, Solving the Hamiltonian path problem with a light-based computer, Natural Computing, 2008
[16] Gerald L. Thompson and Shared Singhal, A probabilistic polynomial Algorithm for solving a directed Hamiltonian path problem, 1983
[17] Omar M. Sallabi and Younis El-Haddad, An Improved Genetic Algorithm to Solve the Traveling Salesman Problem, World Academy of Science, Engineering and Technology, pp. 403-406, 2009
[18] Frank Rubin, a Search Procedure for Hamilton Paths and Circuits, Journal of the ACM, p. 576–80, 1974
[19] Richard Bellman, on a routing problem, Quarterly of Applied Mathematics, p. 87–90, 1958
[20] L. R. Ford Jr., Network Flow Theory, 1956
[21] E. F. Moore, The shortest path through a maze, Proc. Internat. Sympos. Switching Theory 1957, Part II. Cambridge, Mass.: Harvard Univ. Press, p. 285–292, 1959
[22] J. Y. Yen, An algorithm for finding shortest routes from all source nodes to a given destination in general networks, Quarterly of Applied Mathematics, p. 526–530, 1970
[23] Silvia, Jose Daniel and Carlos Llopis, DNA based in silicon (Inchrosil), International Journal of Scientific & Engineering Research, pp. 728-732, 2014.
[24] Silvia, Jose Daniel and Carlos Llopis, Electronic System for emulating the chain of the DNA structure of a chromosome. Spain Patent WO 2009/022024 A1, 19 Febrary 2009.
[25] Foreman, Matthew and Akihiro Kanamori, Handbook of Set Theory, 2010.
[26] M. Morris Mano, Digital Logic and Computer Design, Prentice-Hall, 1979
[27] C. S. Wallace, A suggestion for a fast multiplier, IEEE Trans. on Electronic Comp, 1964.





No comments:
Post a Comment